MATH167R: Simulation based inference

Peter Gao

Overview of today

• Sampling distributions
• Bootstrap distributions

Sampling distributions

Without explicitly saying so, we have been simulating sampling distributions during our simulations.

Recall: A sampling distribution is the probability distribution of a sample-based statistic.

Example: If \(X_1,\ldots, X_{100}\) are iid random variables with variance \(1\), what is the distribution of the sample mean \(\overline{X}\)?

Simulating a sampling distribution

Example simulation: Suppose \(X_1,\ldots, X_{100}\sim N(0,1)\).

set.seed(123)
Xbar <- replicate(10000, mean(rnorm(100)))
hist(Xbar, main = "Sampling distribution of mean of 100 N(0, 1) variables")

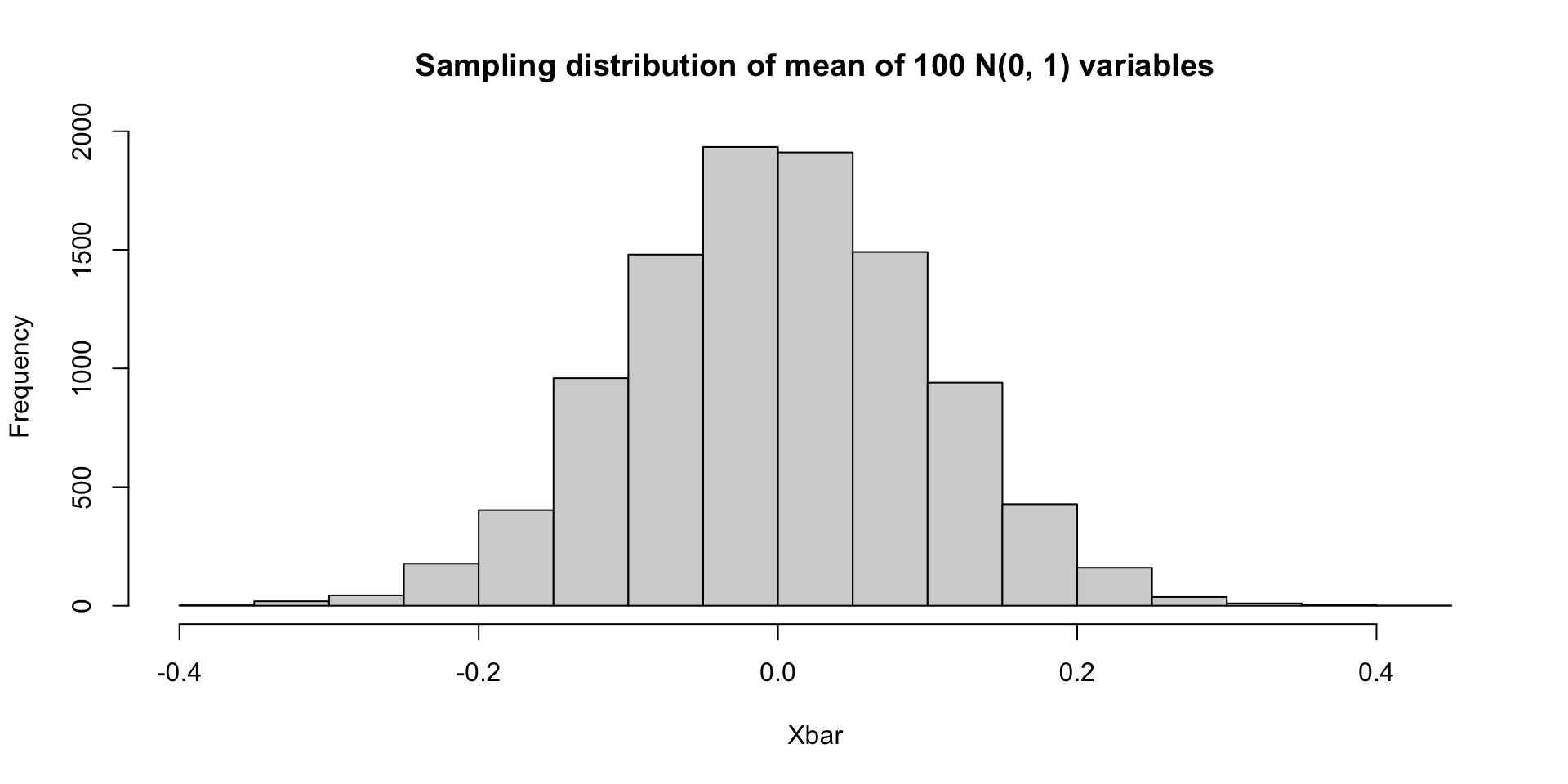
Simulating a sampling distribution

What if \(X_1,\ldots, X_{100}\sim \mathrm{Exp}(1)\)?

set.seed(123)
Xbar <- replicate(10000, mean(rexp(100, rate = 1)))
hist(Xbar, main = "Sampling distribution of mean of 100 Exponential(1) variables")

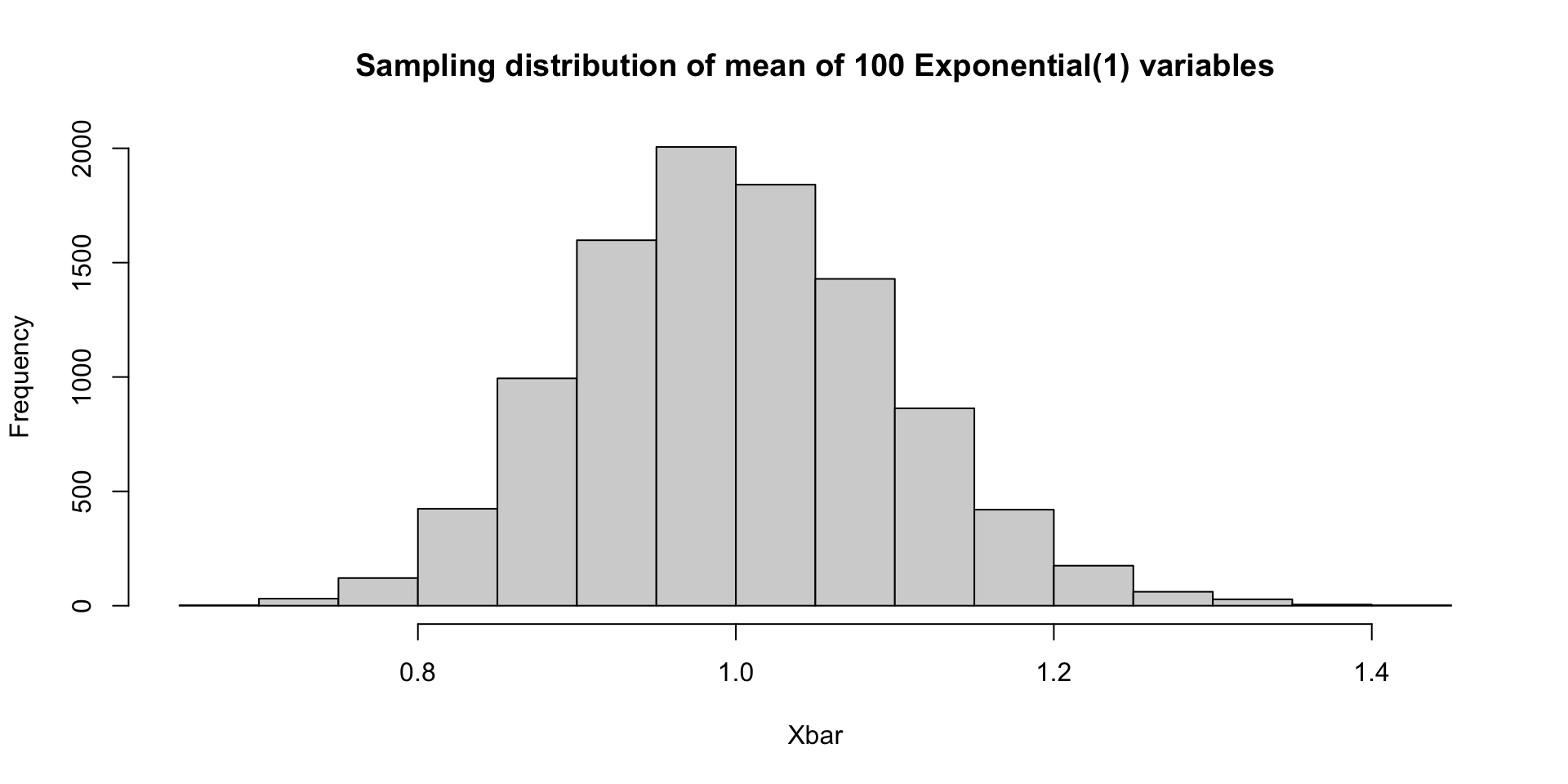
Simulating a sampling distribution

What if \(X_1,\ldots, X_{100}\sim \mathrm{Poisson}(1)\)?

set.seed(123)
Xbar <- replicate(10000, mean(rpois(100, lambda = 1)))
hist(Xbar, main = "Sampling distribution of mean of 100 Poisson(1) variables")

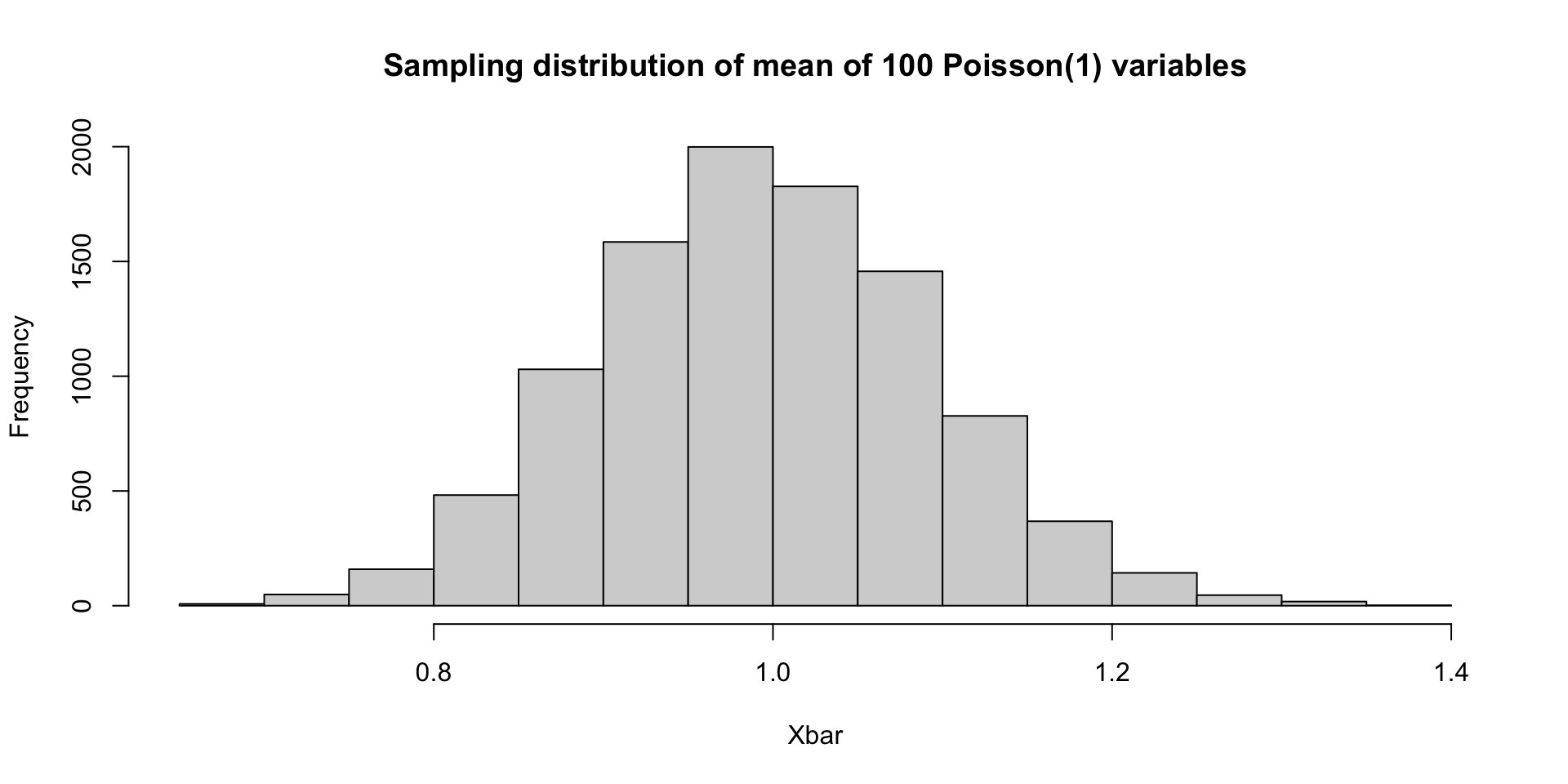
Simulating a sampling distribution

By the central limit theorem, all of these sampling distributions are asymptotically Gaussian with variance 1/100 (though the mean values differ between the three). Since \(n=100\) is fairly large (for these examples), all of the previous examples are close to Gaussian.

What about if \(n\) is smaller? Or if we consider other distributions?

Simulation is a powerful strategy for testing out methods:

• Suppose you wish to know… is \(n\) large?
• Create a simulation that generates data that looks like your real world data.
• Evaluate whether the results are reasonable/accurate using simulated data.

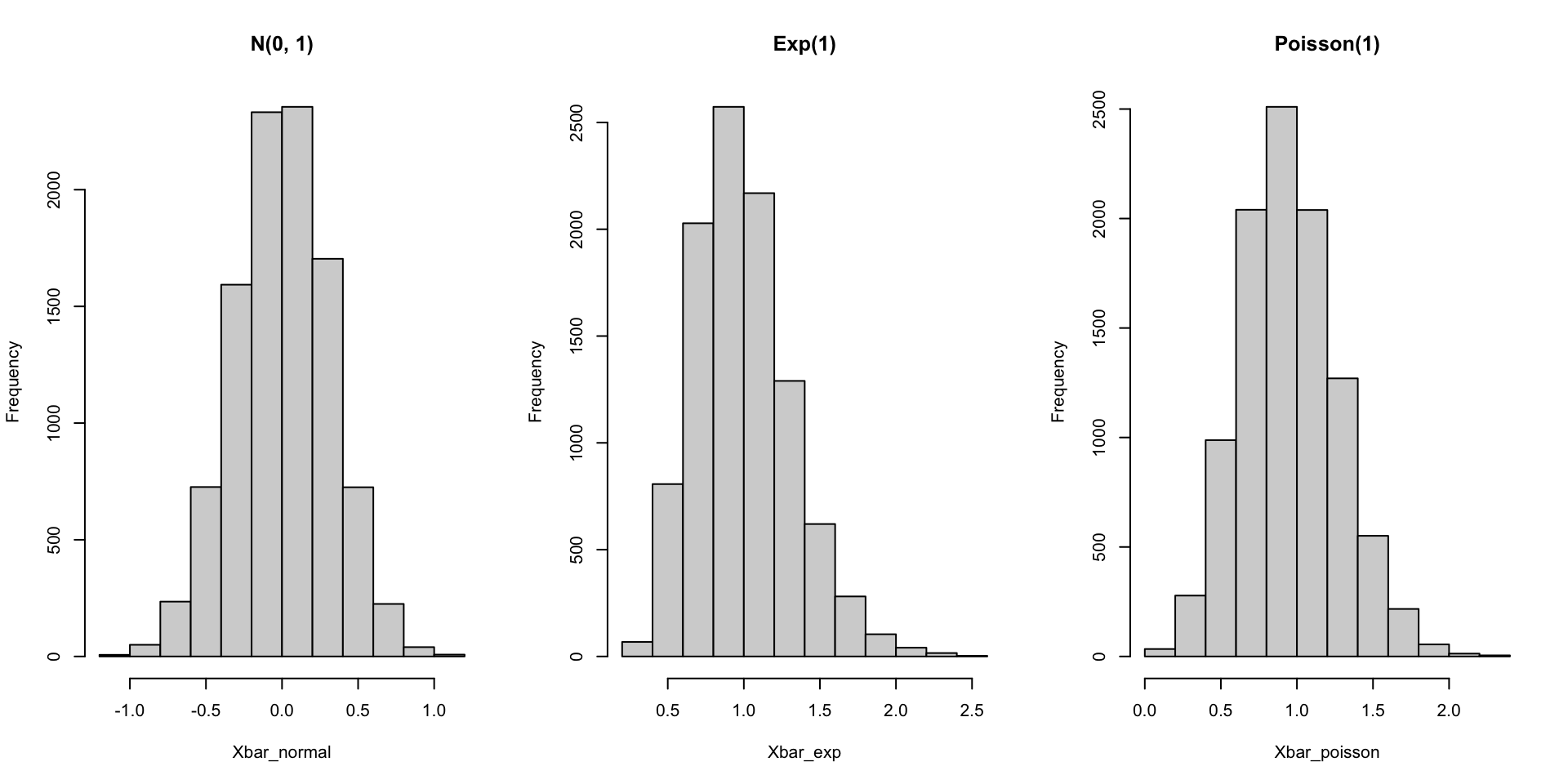
Smaller sample sizes

set.seed(123)
Xbar_normal <- replicate(10000, mean(rnorm(10)))
Xbar_exp <- replicate(10000, mean(rexp(10, rate = 1)))
Xbar_poisson <- replicate(10000, mean(rpois(10, lambda = 1)))
par(mfrow = c(1, 3))
hist(Xbar_normal, main = "N(0, 1)")
hist(Xbar_exp, main = "Exp(1)")
hist(Xbar_poisson, main = "Poisson(1)")

Smaller sample sizes

Other statistics

What if we want the sampling distribution of the maximum? For each of these population models, the sampling distribution of the maximum is different.

set.seed(123)
Xmax_normal <- replicate(10000, max(rnorm(10)))
Xmax_exp <- replicate(10000, max(rexp(10, rate = 1)))
Xmax_poisson <- replicate(10000, max(rpois(10, lambda = 1)))
par(mfrow = c(1, 3))
hist(Xmax_normal, main = "N(0, 1)")
hist(Xmax_exp, main = "Exp(1)")
hist(Xmax_poisson, main = "Poisson(1)")

Other statistics

What if we want the sampling distribution of the maximum? For each of these population models, the sampling distribution of the maximum is different.

Transformations

We can easily simulate sampling distributions for statistics summarizing the distribution of random variables that are defined as transformations of other random variables.

set.seed(123)
Xbar_normal <- replicate(10000, mean(rnorm(10) ^ 2))
Xbar_exp <- replicate(10000, mean(rexp(10, rate = 1) ^ 2))
Xbar_poisson <- replicate(10000, mean(rpois(10, lambda = 1) ^ 2))
par(mfrow = c(1, 3))
hist(Xbar_normal, main = "N(0, 1) squared")
hist(Xbar_exp, main = "Exp(1) squared")
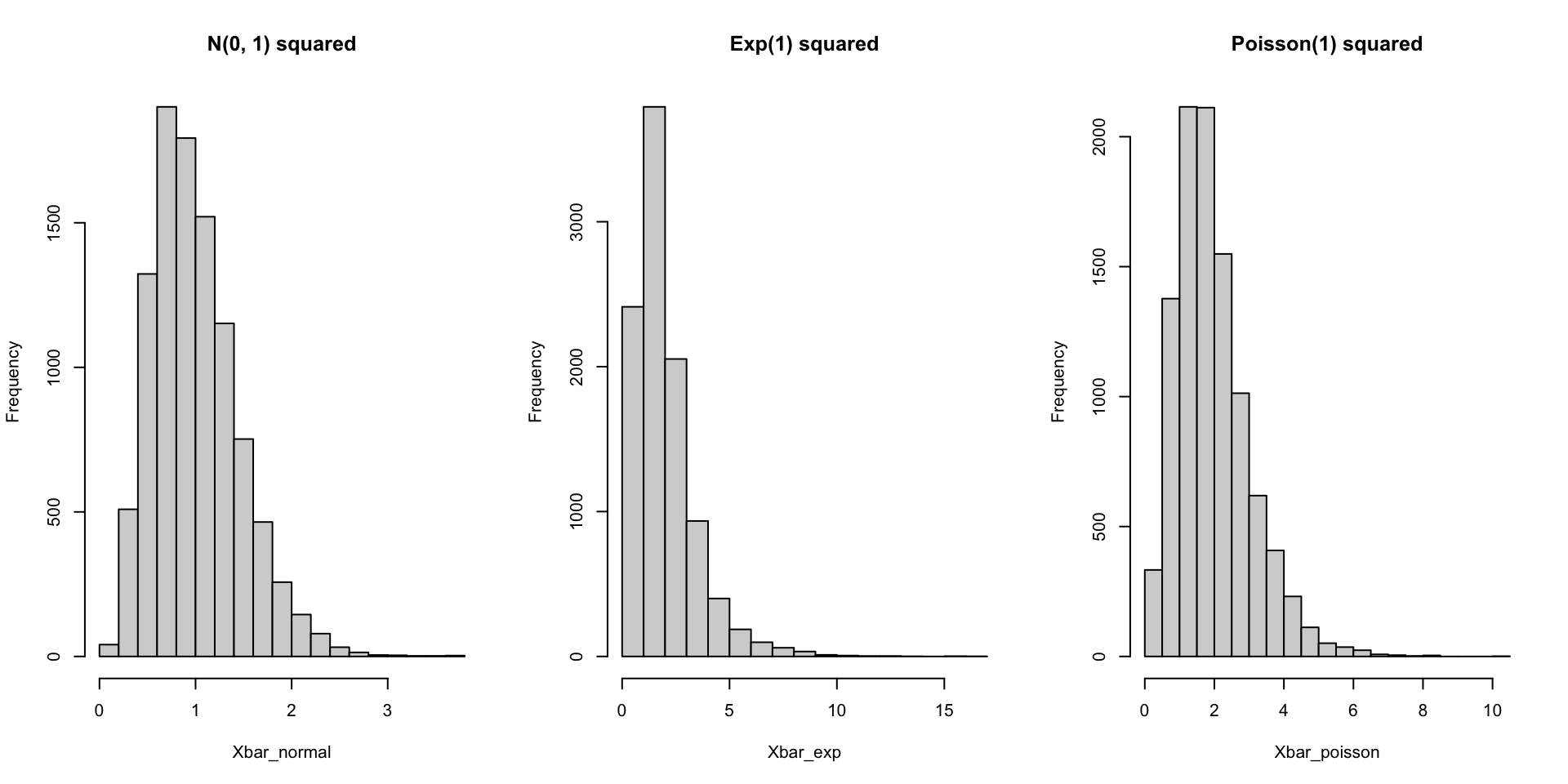
hist(Xbar_poisson, main = "Poisson(1) squared")

Transformations

We can easily simulate sampling distributions for statistics summarizing the distribution of random variables that are defined as transformations of other random variables.

Exercise

• Write code to create a histogram of the sampling distribution of the sample mean \(\overline{Y}\) of \(Y_1,\ldots, Y_{10}\) where \(Y_i=\sin(X_i)\) and \(X_1,\ldots, X_{10}\) are iid Uniform(0, 1) random variables.

Resampling methods

The previous simulations are all based on parametric models (normal, exponential, Poisson). However, we can also simulate sampling distributions without parametric assumptions on the data generating mechanism.

Estimating the age of US pennies

Suppose we want to estimate the average age of US pennies. We can’t observe every single penny—so what if we take a sample of 50 pennies?

Based on an example from ModernDive.

Estimating the age of US pennies

The moderndive package contains data on a sample of 50 pennies in the pennies_sample data frame.

library(moderndive)
data(pennies_sample)
head(pennies_sample)

# A tibble: 6 × 2
     ID  year
  <int> <dbl>
1     1  2002
2     2  1986
3     3  2017
4     4  1988
5     5  2008
6     6  1983

Estimating the age of US pennies

The moderndive package contains data on a sample of 50 pennies in the pennies_sample data frame.

library(tidyverse)
ggplot(pennies_sample, aes(x = year)) +
  geom_histogram(binwidth = 10, color = "white") +
  theme_minimal()

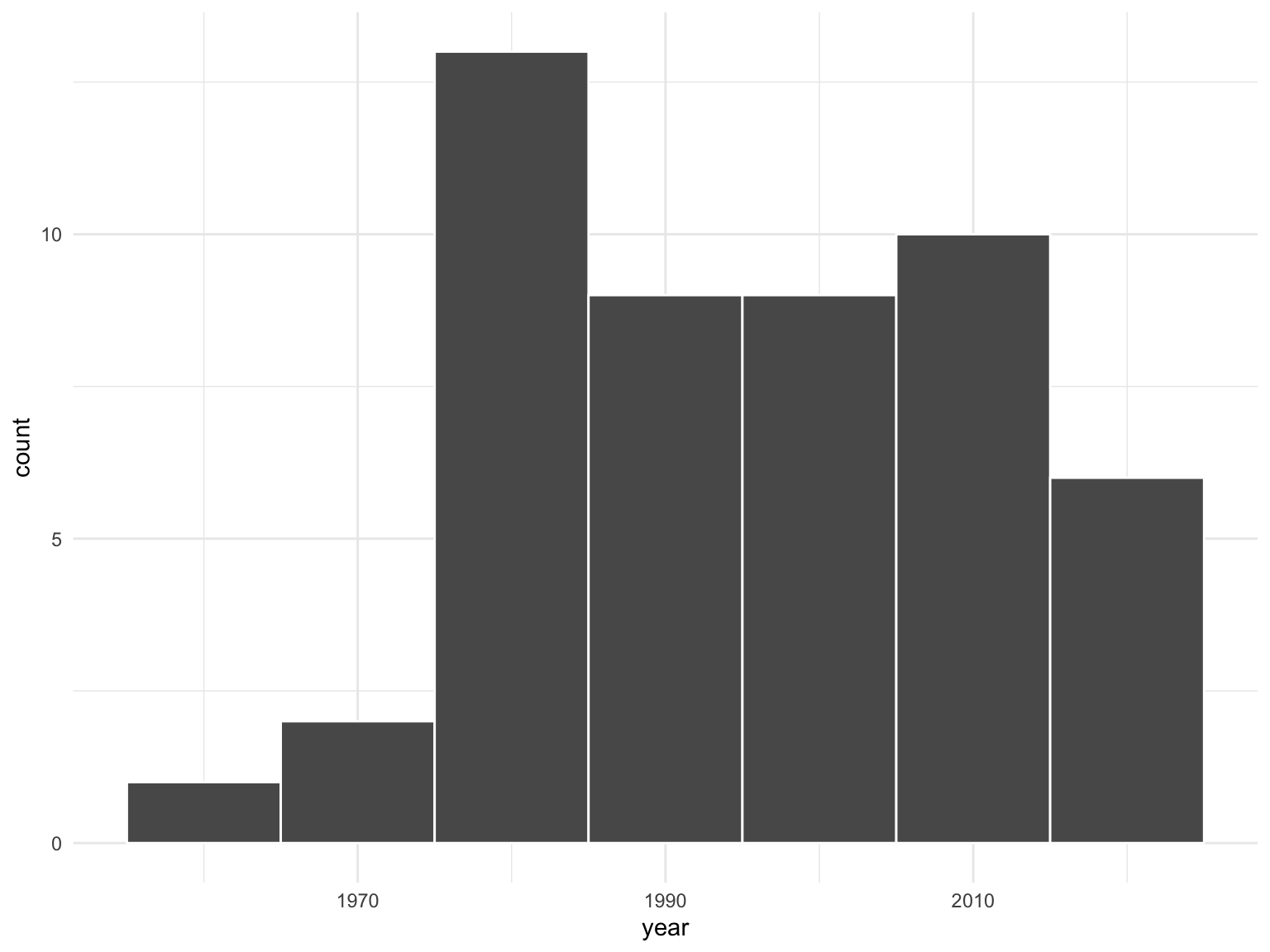
Estimating the age of US pennies

Based on this sample, we can compute the sample mean:

x_bar <- pennies_sample |>
  summarize(mean_year = mean(year))
x_bar

# A tibble: 1 × 1
  mean_year
      <dbl>
1     1995.

Resampling the pennies

Imagine we put our 50 pennies in a bag and draw a new sample of 50 pennies by sampling with replacement. This is called resampling with replacement.

set.seed(327)
pennies_resample <-
  data.frame(year = sample(pennies$year, 50, replace = T))
head(pennies_resample)

  year
1 1973
2 1977
3 1976
4 2004
5 1981
6 2000

pennies_resample %>% 
  summarize(mean_year = mean(year))

  mean_year
1   1987.58

Resampling the pennies

Imagine we put our 50 pennies in a bag and draw a new sample of 50 pennies by sampling with replacement. This is called resampling with replacement.

pennies_combined <- 
  bind_rows(pennies_sample |> mutate(title = "Original sample"),
            pennies_resample |> mutate(title = "Resample"))
ggplot(pennies_combined, aes(x = year)) +
  geom_histogram(binwidth = 10, color = "white") +
  facet_wrap(~title) + 
  theme_minimal()

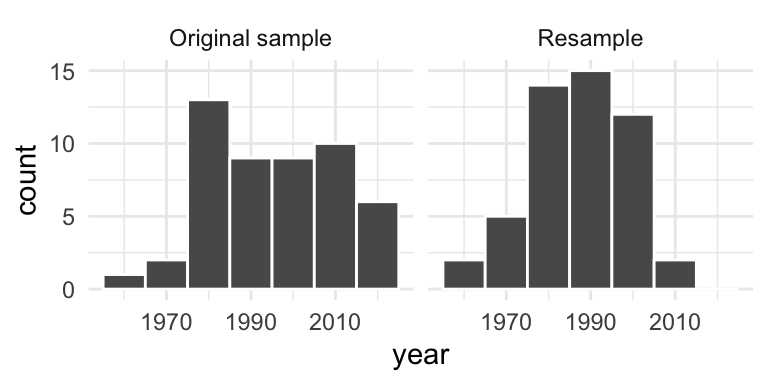
Resampling the pennies

Note that our resample is not the same as drawing a new sample from the population. However, we can still learn about the sampling variability of the sample mean. Suppose we repeat this process many times.

head(pennies_resamples)

# A tibble: 6 × 3
# Groups:   name [1]
  replicate name     year
      <int> <chr>   <dbl>
1         1 Arianna  1988
2         1 Arianna  2002
3         1 Arianna  2015
4         1 Arianna  1998
5         1 Arianna  1979
6         1 Arianna  1971

Resampling the pennies

We can compute each resample mean:

resampled_means <- pennies_resamples |>
  group_by(name) |>
  summarize(mean_year = mean(year))
head(resampled_means)

# A tibble: 6 × 2
  name      mean_year
  <chr>         <dbl>
1 Arianna       1992.
2 Artemis       1996.
3 Bea           1996.
4 Camryn        1997.
5 Cassandra     1991.
6 Cindy         1995.

Resampling the pennies

We can compute each resample mean:

ggplot(resampled_means, aes(x = mean_year)) +
  geom_histogram(binwidth = 1, color = "white", boundary = 1990) +
  labs(x = "Sampled mean year") +
  theme_minimal()

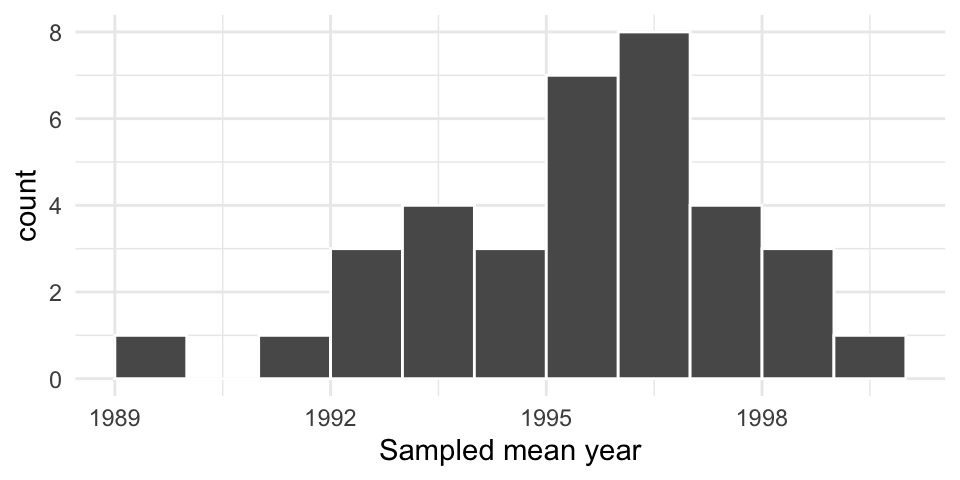
Resampling the pennies 1000 times

Using simulation, we can repeat this process virtually 1000 times:

# Repeat resampling 1000 times
virtual_resamples <- pennies_sample |>
  rep_sample_n(size = 50, replace = TRUE, reps = 1000)

# Compute 1000 sample means
virtual_resampled_means <- virtual_resamples |>
  group_by(replicate) |>
  summarize(mean_year = mean(year))

Resampling the pennies 1000 times

Using simulation, we can repeat this process virtually 1000 times:

ggplot(virtual_resampled_means, aes(x = mean_year)) +
  geom_histogram(binwidth = 1, color = "white", boundary = 1990) +
  labs(x = "sample mean") +
  theme_minimal()

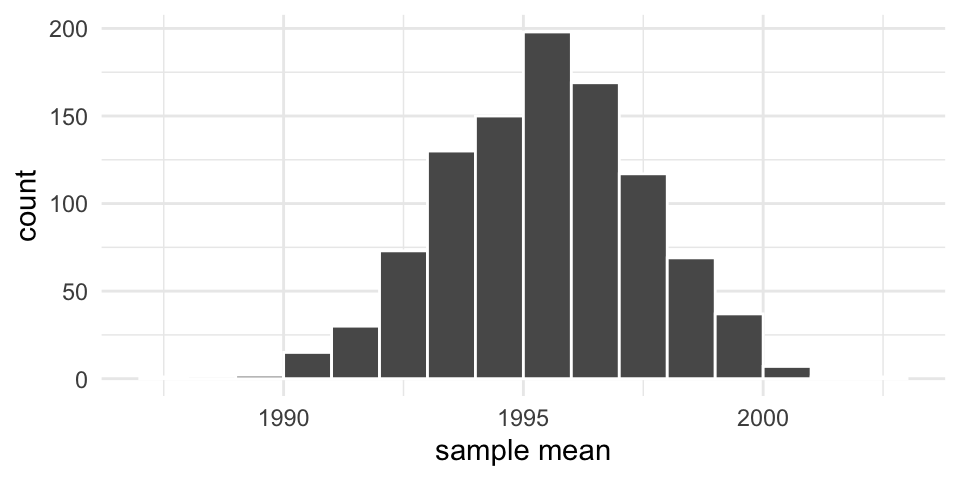
Resampling the pennies 1000 times

Note that our resampled means are centered around our original sample mean. This means that resampling doesn’t tell us about how far off our particular sample is–only about the variability of the observed values.

virtual_resampled_means |>
  summarize(mean_of_means = mean(mean_year))

# A tibble: 1 × 1
  mean_of_means
          <dbl>
1         1995.

mean(pennies_sample$year)

[1] 1995.44

Resampling confidence intervals

We can obtain a confidence interval based on our resample means:

quantile(virtual_resampled_means$mean_year, c(.025, .975))

    2.5%    97.5% 
1991.358 1999.441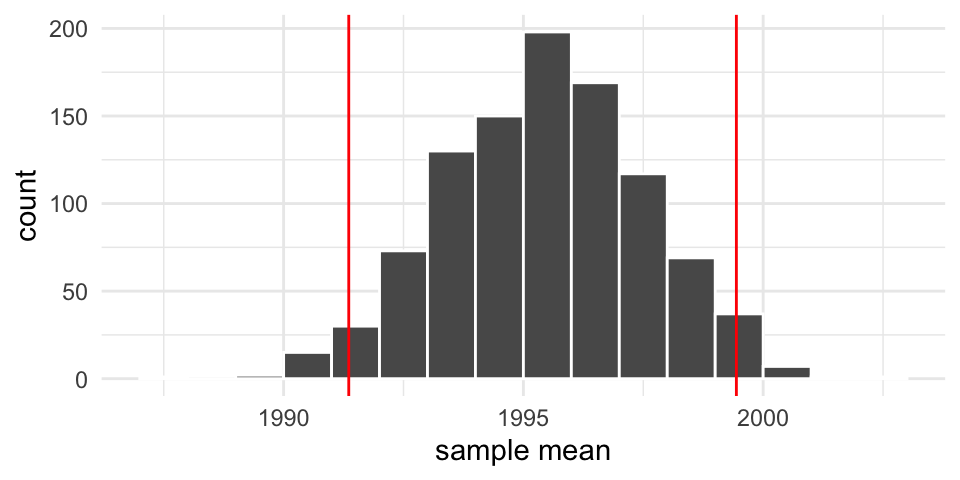 

ggplot(virtual_resampled_means, aes(x = mean_year)) +
  geom_histogram(binwidth = 1, color = "white", boundary = 1990) +
  geom_vline(xintercept = quantile(virtual_resampled_means$mean_year, c(.025, .975)), 
             color = 'red') +
  labs(x = "sample mean") +
  theme_minimal()

Resampling confidence intervals

Compare with a normal sampling distribution based confidence interval:

virtual_resampled_means |>
  summarize(lower = mean(mean_year) - 1.96 * sd(mean_year),
            upper = mean(mean_year) + 1.96 * sd(mean_year))

# A tibble: 1 × 2
  lower upper
  <dbl> <dbl>
1 1991. 2000.

Resampling methods

Suppose we know \(X_1,\ldots, X_{20}\sim \mathrm{Exp}(1)\). The sampling distribution of the sample mean can be simulated as follows:

set.seed(123)
Xbar_exp <- replicate(10000, mean(rexp(20, rate = 1)))
hist(Xbar_exp)

Resampling methods

What if we observe \(X_1,\ldots, X_{20}\), but we don’t know that \(X_i\) is exponentially distributed? We could just try the normal approximation to approximate the sampling distribution.

X <- rexp(20, rate = 1)
x_axis <- seq(0, 3, length.out = 1000)

# plot "true" simulated sampling distribution
hist(Xbar_exp, freq = F, ylim = c(0, 3))

# plot normal theory
lines(x_axis, dnorm(x_axis, mean = mean(X), sd = sd(X) / sqrt(20)), col = 'red')

Resampling methods

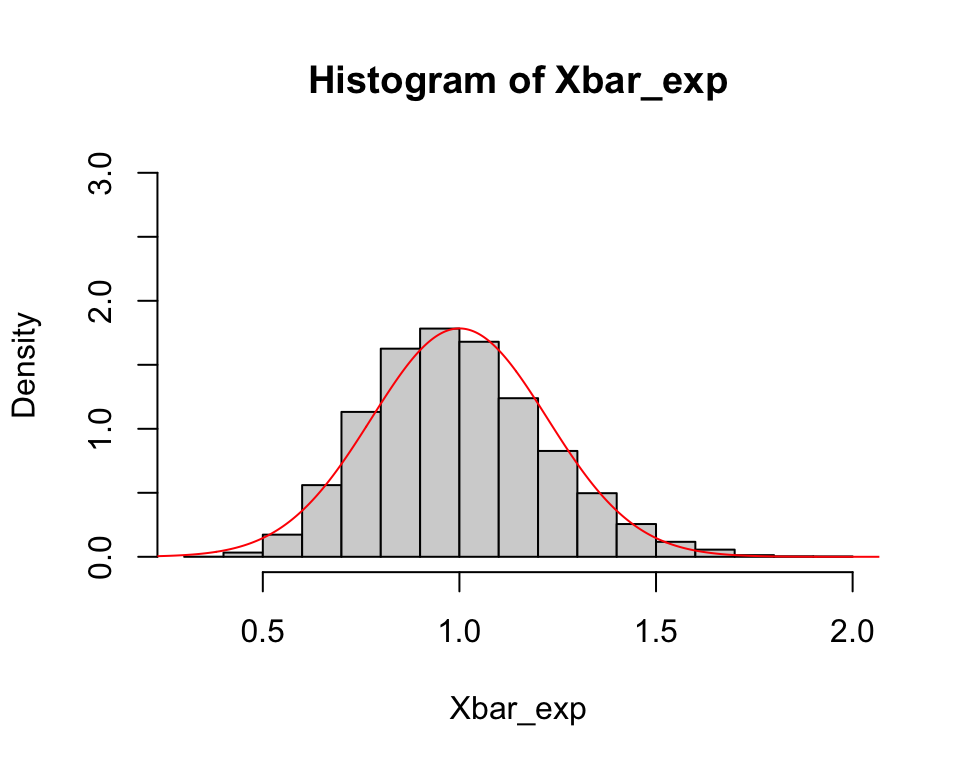
Bootstrap samples

Bootstrapping is a resampling method that uses random samples with replacement from the sample data to approximate the sampling distribution of sample-based statistics.

print(sort(X))

 [1] 0.00816693 0.06263315 0.11949335 0.12600941 0.14474580 0.14660666
 [7] 0.15582213 0.17485277 0.23514296 0.35492087 0.48980207 0.52215538
[13] 0.72200938 1.27034542 1.56551624 1.74866229 1.82459209 1.84311722
[19] 2.14225230 2.24995288

# sample with replacement from X
X_resample <- sample(X, size = 20, replace = TRUE)
print(sort(X_resample))

 [1] 0.06263315 0.11949335 0.11949335 0.11949335 0.11949335 0.12600941
 [7] 0.14474580 0.14474580 0.15582213 0.15582213 0.17485277 0.35492087
[13] 0.35492087 0.48980207 0.72200938 0.72200938 1.56551624 2.14225230
[19] 2.24995288 2.24995288

Bootstrap samples

We can repeatedly resample from \(X\), then compute the resample sample means and plot the distribution:

bootstrap_Xbar <- replicate(10000, mean(sample(X, size = 20, replace = TRUE)))
hist(bootstrap_Xbar - mean(X) + 1)

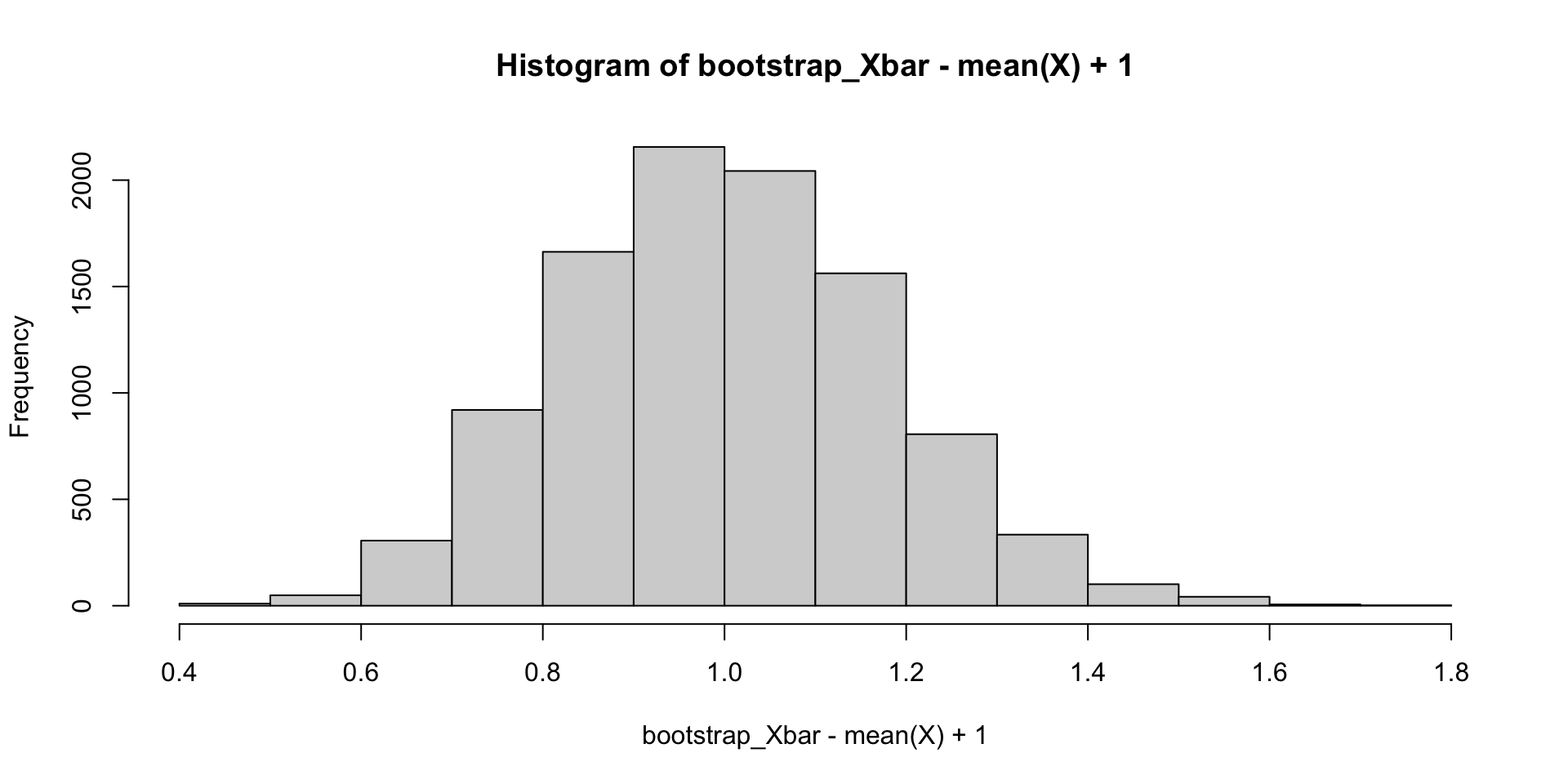
Bootstrap samples

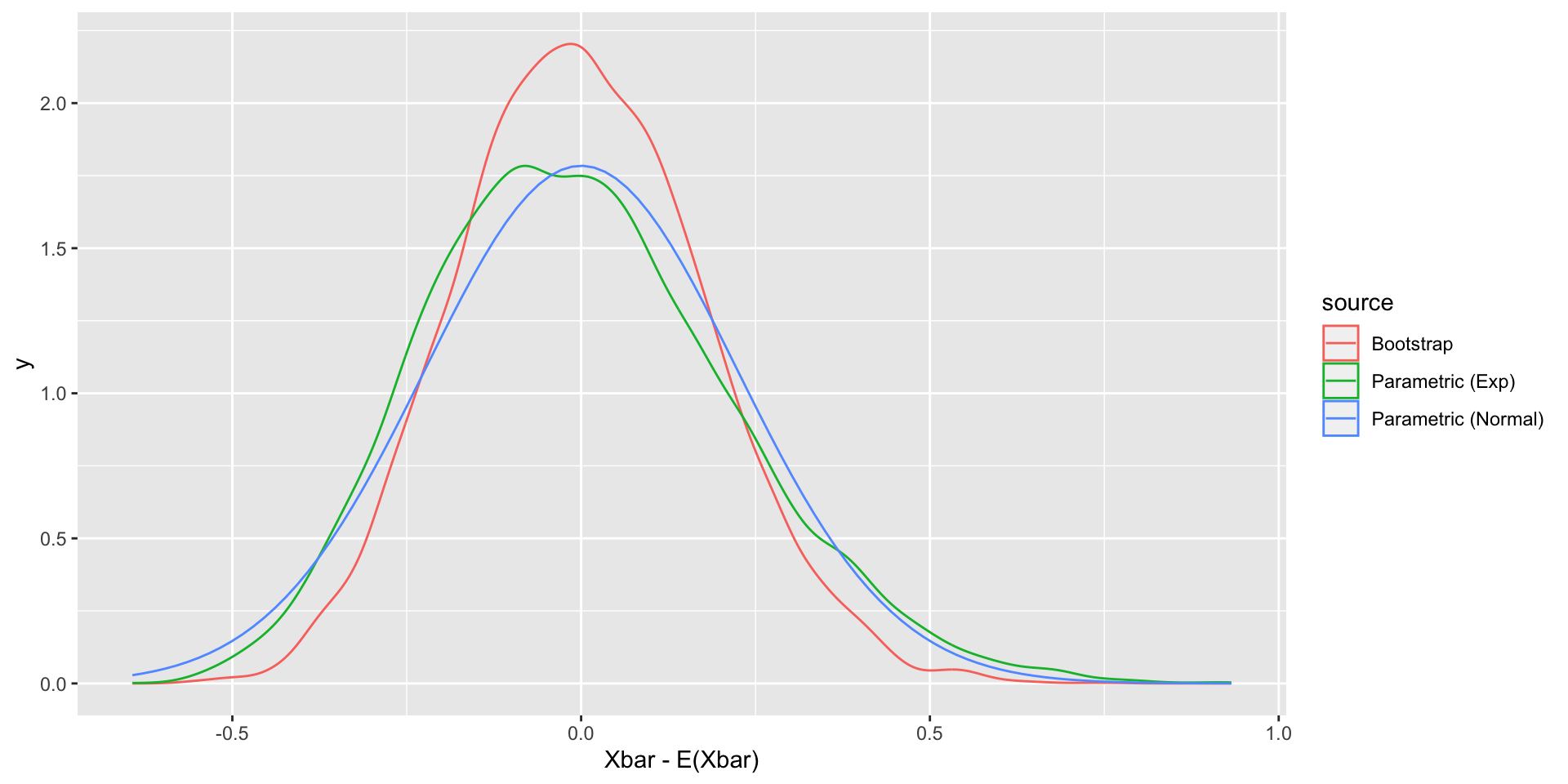
We can compare the bootstrap sampling distributions and true sampling distributions for \(\overline{X}-E(\overline{X})\).

library(ggplot2)
plot_dat <-
  data.frame(Xbar = c(Xbar_exp - 1, bootstrap_Xbar - mean(X)),
             source = rep(c("Parametric (Exp)", "Bootstrap"), each = 10000))
ggplot(plot_dat, aes(x = Xbar, color = source)) +
  geom_density() +
  geom_function(fun = dnorm, 
                args = list(mean = 0, sd = 1 / sqrt(20)),
                aes(color = "Parametric (Normal)")) +
  xlab("Xbar - E(Xbar)")

Bootstrap samples

We can compare the bootstrap sampling distributions and true sampling distributions for \(\overline{X}-E(\overline{X})\).

Bootstrap confidence intervals

We can take appropriate quantiles of the bootstrap samples to construct a bootstrap confidence interval using the quantile() function:

quantile(bootstrap_Xbar, probs = c(.025, .975))

    2.5%    97.5% 
0.467759 1.157051 

Why bootstrap?

In this case, inference based on bootstrapping does not seem better than the normal approximation based on the central limit theorem.

However, for many cases, we may not have a simple parametric approximation to the true sampling distribution. For example, suppose we wish to compute the sampling distribution of the sample median.

Note however that the bootstrap may not work well for all statistics, such as the minimum (why not?).