Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.07939
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean in group 1 mean in group 2
0.75 2.33 MATH167R: Hypothesis Testing
Overview of today
- Review of basic hypothesis tests
- Designing your own hypothesis test
- Permutation tests
Summary: hypothesis testing
Define null and alternative hypotheses.
- ex. \(H_0:\mu = 0\) and \(H_a:\mu\neq 0\)
Compute a test statistic for which the null sampling distribution is known (based on assumptions about the population/sample).
- ex. \(T=(\overline{X}_n-\mu)/(S^2/\sqrt{n})\sim t_{n-1}\)
Compare the test statistic with the null distribution to obtain a P-value.
- ex. \(P(|T|>|t|)\) where \(t\) is the observed test statistic.
Example: Two-sample \(z\)-test
Assumptions:
- \(X_1, \ldots, X_m\) is a random sample from a distribution with mean \(\mu_1\) and variance \(\sigma_1^2\).
- \(Y_1, \ldots, Y_n\) is a random sample from a distribution with mean \(\mu_2\) and variance \(\sigma_2^2\).
- The \(X\) and \(Y\) samples are independent of one another.
- The sample sizes are adequately large (usually appropriate if \(m>40\) and \(n>40\).
Example: Two-sample \(z\)-test
Hypotheses:
- H_0: \(\mu_1=\mu_2\)
- H_a: \(\mu_1\not=\mu_2\)
Example: Two-sample \(z\)-test
Under these assumptions, \(\overline{X}-\overline{Y}\) is approximately normal and the test statistic \[Z=\frac{\overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{m}+\frac{S_2^2}{n}}}\] has approximately a standard normal distribution when \(H_0\) is true.
Example: Two-sample \(t\)-test
When the samples are small, but the population distributions are approximately normal, the standardized test statistic \[T=\frac{\overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{m}+\frac{S_2^2}{n}}}\] has approximately a \(t\) distribution with df \(v\) estimated from the data by
\[\nu =\frac{\left(\frac{s_1^2}{m}+\frac{s_2^2}{n}\right)^2}{\frac{(s_1^2/m)^2}{m-1}+\frac{(s_2^2/n)^2}{n-1}}\]
Example: Two-sample \(t\)-test
We can use the sleep data in R, which contains Student’s example data on the effect of two sleeping drugs on 10 patients, to test out the t.test() function.
“There is only one test”

Image by Allen Downey
“There is only one test”: Tim and Bob

“There is only one test”: Tim and Bob
Image by Allen Downey
What is the data? Test statistic? Model of \(H_0\)? P-value?
Designing your own hypothesis test
Suppose we have five sequences of 200 coin flips.
# A tibble: 6 × 5
A B C D E
<chr> <chr> <chr> <chr> <chr>
1 T H H T H
2 H H H H H
3 T H T H H
4 H T H H H
5 H T T H T
6 T H T T H Only one sequence is generated by flipping a fair coin, using the code sample(c("H", "T"), 200, replace = T).
Can we design a hypothesis test to help us identify the true sequence?
This activity adapted from a blog post from Alex Hayes.
Designing your own hypothesis test
First, load the flips using the following code.
# A tibble: 6 × 5
A B C D E
<chr> <chr> <chr> <chr> <chr>
1 T H H T H
2 H H H H H
3 T H T H H
4 H T H H H
5 H T T H T
6 T H T T H Can you tell which is real and which are fake?
Visual inspection
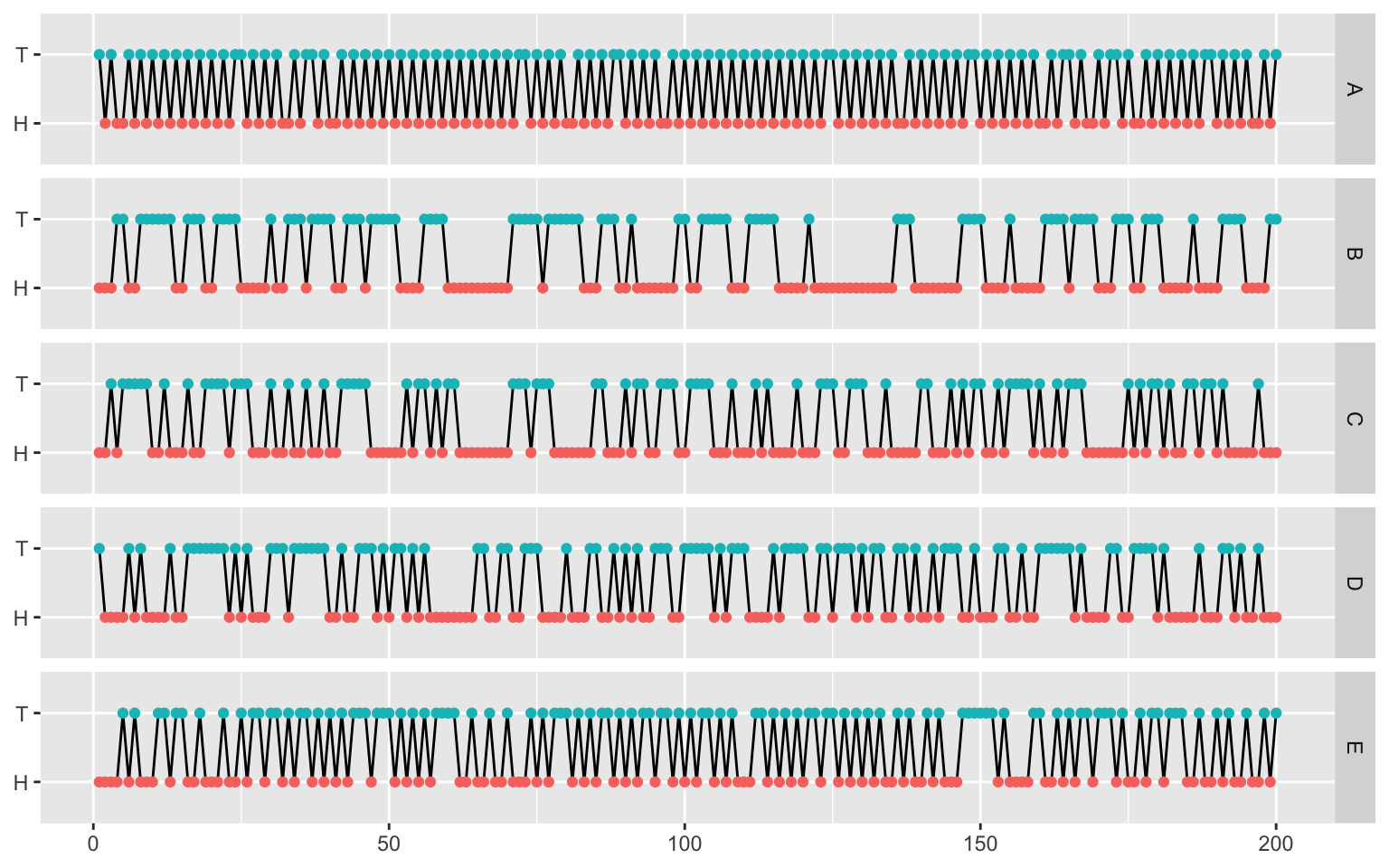
Visual inspection
flips_long <- flips |>
mutate(id = 1:200) |>
pivot_longer(-id, names_to = "Sequence", values_to = "Flip")
flips_long |>
ggplot(aes(x = id, y = Flip, group = Sequence)) +
geom_line() +
geom_point(aes(color = Flip)) +
facet_grid(rows = vars(Sequence)) +
theme(
legend.position = "none",
axis.title = element_blank()
)A simple test: Counting the number of heads
We can use the test we discussed last class for a sample proportion:
\[\begin{align} H_0: p&=1/2\\ H_a: p&\neq 1/2 \end{align}\]where we assume that the flips \(X_1,...,X_n\) are iid \(X_i \stackrel{iid}{\sim} \mathrm{Binomial}(1, p)\) with probability of heads \(p\).
A simple test: Counting the number of heads
What are the test statistics for each of our sequences? One option is to use the total number of heads.
# A tibble: 5 × 2
Sequence nHeads
<chr> <int>
1 A 100
2 B 108
3 C 114
4 D 101
5 E 98A simple test: Counting the number of heads
Do any of these indicate that certain sequences are fake? How could we get corresponding P-values?
Approach one: Use the normal approximation: \[\widehat{p}\sim N\left(p, \sqrt{\frac{p(1-p)}{n}}\right)\]
phats <- flips_long |>
group_by(Sequence) |>
summarize(phat = mean(Flip == "H"))
# two-sided p-values
(1 - pnorm(abs(phats$phat - .5), sd = sqrt(.5 * .5 / 200))) * 2[1] 1.00000000 0.25789904 0.04771488 0.88753708 0.77729741This suggests that sequence C has too many heads.
A simple test: Counting the number of heads
Approach two: Use simulations to estimate the distribution of number of heads under the null:
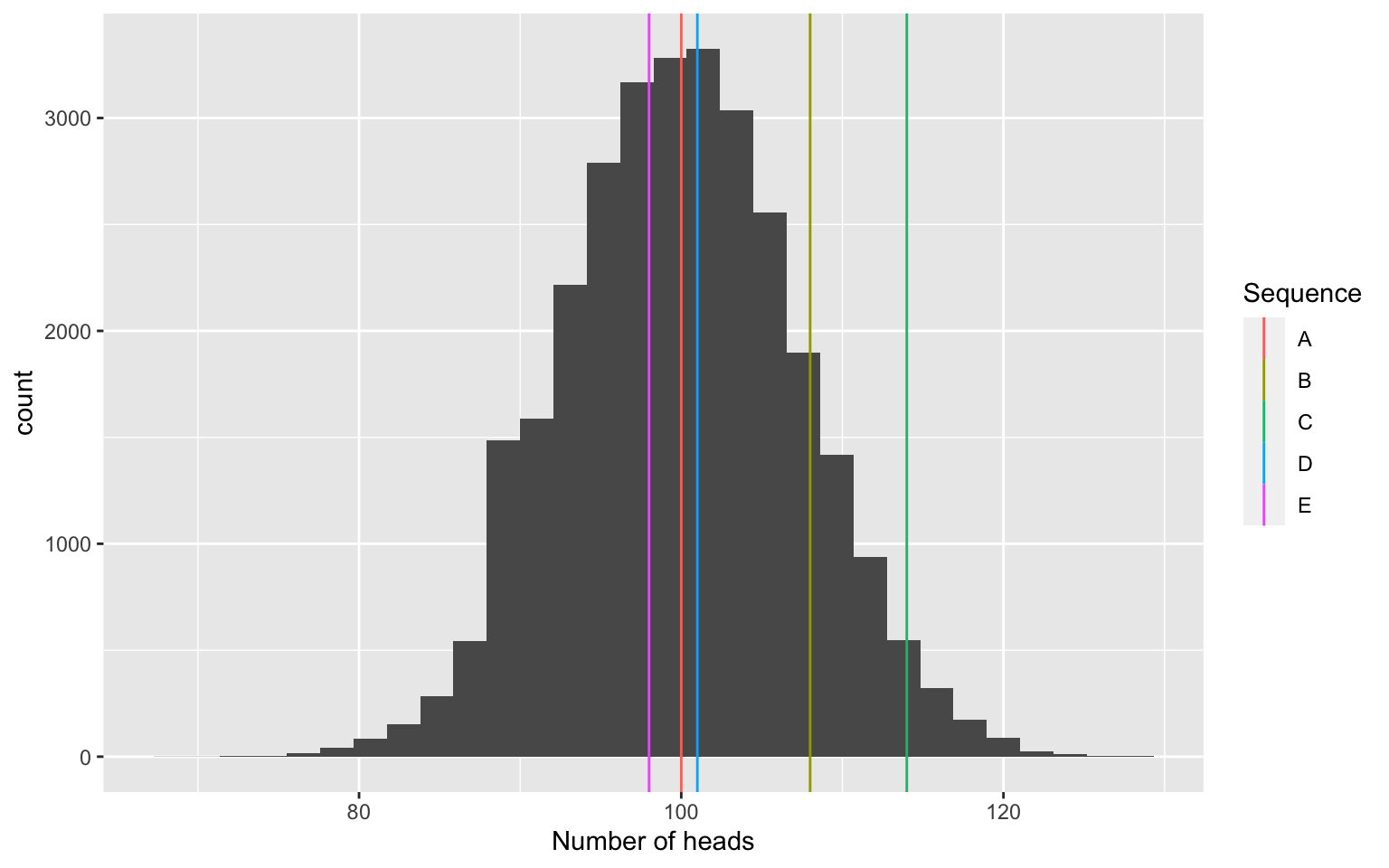
A simple test: Counting the number of heads
Approach two: Use simulations to estimate the distribution of number of heads under the null:
sim_totals <- data.frame(x = rbinom(30000, 200, .5))
flip_totals <- flips_long |>
group_by(Sequence) |>
summarize(nHeads = sum(Flip == "H"))
ggplot() +
geom_histogram(data = sim_totals, aes(x = x)) +
geom_vline(data = flip_totals, aes(color = Sequence, xintercept = nHeads)) +
xlab("Number of heads")A simple test: Counting the number of heads
Approach two: Use simulations to estimate the distribution of number of heads under the null:
A slightly different test: streak length
We can also consider a different test statistic: longest streak.
A slightly different test: streak length
We can then simulate the null distribution of streak length.
A slightly different test: streak length
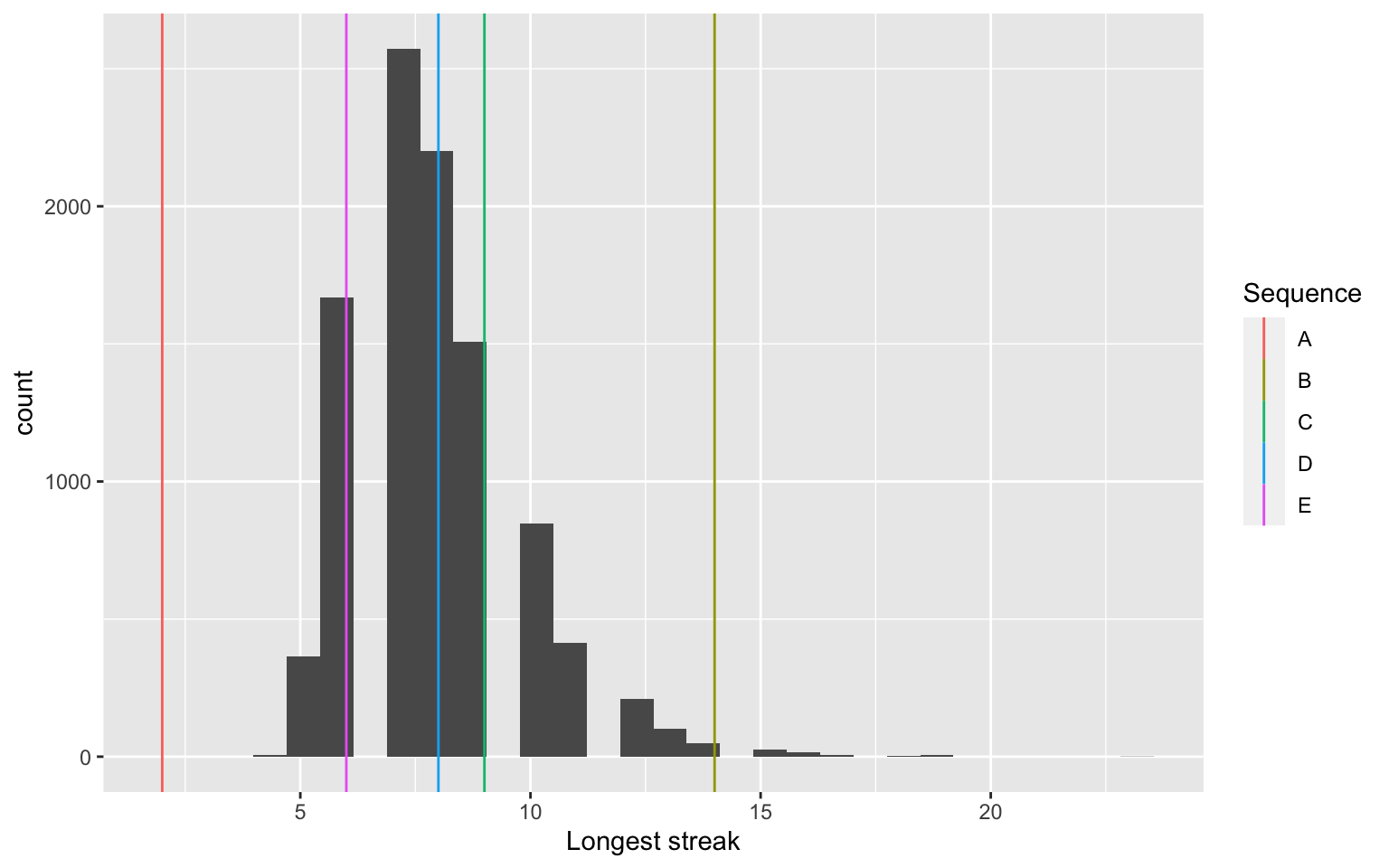
A slightly different test: streak length
Note that calculating the P-value is tricky here–a one-sided test may make the most sense.
[1] 1.0000 0.0057 0.1679 0.3186 0.7961This suggests that the longest streaks are too long for sequence B. Note that we could try other test statistics. What about average streak length?
Designing your own hypothesis test
- Come up with your own test statistic.
- Simulate the null distribution of your test statistic.
- Can you identify which sequence is the real one?
P-Hacking: Designing a test after seeing the data
In principle, we should decide which test to use before seeing the data. Why?
I could use the following test statistic: number of times the exact sequence \(D\) is obtained. What is the P-value for each sequence?